DDPP5 第三章 “ Switching Algebra and Combinational Logic” 的学习笔记。
本章的主要内容为逻辑代数、 逻辑代数在电路中的使用及化简、 timing hazard。
Switching Algebra 这一节基本上就是离散数学 (1) 开头两章的内容， 术语和记号有很多不同， 幸好忘的差不多了， 不然都要搞混了 。
记号
AND： X ⋅ Y X\ \cdot\ Y X ⋅ Y
： X + Y X + Y X + Y NOT： X ′ X' X ′
AND 的优先级高于 OR
（ yysy 我还是更喜欢 ∨ , ∧ \lor, \land ∨ , ∧ ， ⋅ \cdot ⋅ ， + + + 。 ） （ 它们明明是对偶的怎么搞得像个环一样。 ） （ 主要还是下面这些定理用加号看起来真的好怪。 ） （ 异或不是还号称二进制加法吗。 ）
公理 (A1) X ≠ 1 ⟹ X = 0 (A1D) X ≠ 0 ⟹ X = 1 (A2) X = 0 ⟹ X ′ = 1 (A2D) X = 1 ⟹ X ′ = 0 (A3) 0 ⋅ 0 = 0 (A3D) 1 + 1 = 1 (A4) 1 ⋅ 1 = 1 (A4D) 0 + 0 = 0 (A5) 0 ⋅ 1 = 1 ⋅ 0 = 0 (A5D) 1 + 0 = 0 + 1 = 1 \begin{array}{rl}
\text{(A1)} & X \ne 1 \implies X = 0 \\
\text{(A1D)} & X \ne 0 \implies X = 1 \\\\
\text{(A2)} & X = 0 \implies X' = 1 \\
\text{(A2D)} & X = 1 \implies X' = 0 \\\\
\text{(A3)} & 0 \ \cdot\ 0 = 0 \\
\text{(A3D)} & 1 + 1 = 1 \\\\
\text{(A4)} & 1 \ \cdot\ 1 = 1 \\
\text{(A4D)} & 0 + 0 = 0 \\\\
\text{(A5)} & 0 \ \cdot\ 1 = 1 \ \cdot\ 0 = 0 \\
\text{(A5D)} & 1 + 0 = 0 + 1 = 1
\end{array} (A1) (A1D) (A2) (A2D) (A3) (A3D) (A4) (A4D) (A5) (A5D) X = 1 ⟹ X = 0 X = 0 ⟹ X = 1 X = 0 ⟹ X ′ = 1 X = 1 ⟹ X ′ = 0 0 ⋅ 0 = 0 1 + 1 = 1 1 ⋅ 1 = 1 0 + 0 = 0 0 ⋅ 1 = 1 ⋅ 0 = 0 1 + 0 = 0 + 1 = 1 定理 中文名来自《 数理逻辑与集合论（ 第二版） 》 2.2 节“ 等值公式” 。
(T1) X + 0 = X (T1D) X ⋅ 1 = X Identities（同一律） (T2) X + 1 = 1 (T2D) X ⋅ 0 = 0 Null elements（零律） (T3) X + X = X (T3D) X ⋅ X = X Idempotency（幂等律） (T4) ( X ′ ) ′ = X Involution（双重否定律） (T5) X + X ′ = 1 (T5D) X ⋅ X ′ = 0 Complements（补余律） (T6) X + Y = Y + X (T6D) X ⋅ Y = Y ⋅ X Commutativity（交换律） (T7) ( X + Y ) + Z = X + ( Y + Z ) (T7D) ( X ⋅ Y ) ⋅ Z = X ⋅ ( Y ⋅ Z ) Associativity（结合律） (T8) X ⋅ ( Y + Z ) = X ⋅ Y + X ⋅ Z (T8D) X + Y ⋅ Z = ( X + Y ) ⋅ ( X + Z ) Distributivity（分配律） (T9) X + X ⋅ Y = X (T9D) X ⋅ ( X + Y ) = X Covering（吸收律） (T10) X ⋅ Y + X ⋅ Y ′ = X (T10D) ( X + Y ) ⋅ ( X + Y ′ ) = X Combining (T11) X ⋅ Y + X ′ ⋅ Z + Y ⋅ Z = X ⋅ Y + X ′ ⋅ Z (T11D) ( X + Y ) ⋅ ( X ′ + Z ) ⋅ ( Y + Z ) = ( X + Y ) ⋅ ( X ′ + Z ) Consensus (T12) X + X + ⋯ + X = X (T12D) X ⋅ X ⋅ ⋯ ⋅ X = X Generalized idempotency (T13) ( X ⋅ X ⋅ ⋯ ⋅ X ) ′ = X ′ + X ′ + ⋯ + X ′ (T13D) ( X + X + ⋯ + X ) ′ = X ′ ⋅ X ′ ⋅ ⋯ ⋅ X ′ DeMorgan’s theorem （摩根律） (T14) [ F ( X 1 , X 2 , … , X n , + , ⋅ ) ] ′ = F ( X 1 ′ , X 2 ′ , … , X n ′ , ⋅ , + ) Generalized DeMorgan’s theorem \begin{array}{ll}
\begin{array}{rl}
\enspace\text{(T1)} & X + 0 = X \\
\enspace\text{(T1D)} & X \ \cdot\ 1 = X
\end{array}
& \text{Identities（同一律）}
\\\\
\begin{array}{rl}
\enspace\text{(T2)} & X + 1 = 1 \\
\enspace\text{(T2D)} & X \ \cdot\ 0 = 0
\end{array}
& \text{Null elements（零律）}
\\\\
\begin{array}{rl}
\enspace\text{(T3)} & X + X = X \\
\enspace\text{(T3D)} & X \ \cdot\ X = X
\end{array}
& \text{Idempotency（幂等律）}
\\\\
\begin{array}{rl}
\quad\ \text{(T4)} & (X')' = X
\end{array}
& \text{Involution（双重否定律）}
\\\\
\begin{array}{rl}
\enspace\text{(T5)} & X + X' = 1 \\
\enspace\text{(T5D)} & X \ \cdot\ X' = 0
\end{array}
& \text{Complements（补余律）}
\\\\
\begin{array}{rl}
\enspace\text{(T6)} & X + Y = Y + X \\
\enspace\text{(T6D)} & X \ \cdot\ Y = Y \ \cdot\ X
\end{array}
& \text{Commutativity（交换律）}
\\\\
\begin{array}{rl}
\enspace\text{(T7)} & (X + Y) + Z = X + (Y + Z) \\
\enspace\text{(T7D)} & (X \ \cdot\ Y) \ \cdot\ Z = X \ \cdot\ (Y \ \cdot\ Z)
\end{array}
& \text{Associativity（结合律）}
\\\\
\begin{array}{rl}
\enspace\text{(T8)} & X \ \cdot\ (Y + Z) = \,\: X \ \cdot\ Y \,\: + \,\: X \ \cdot\ Z \,\: \\
\enspace\text{(T8D)} & X + \,\: Y \ \cdot\ Z \,\: = (X + Y) \ \cdot\ (X + Z)
\end{array}
& \text{Distributivity（分配律）}
\\\\
\begin{array}{rl}
\enspace\text{(T9)} & X + \,\: X \ \cdot\ Y \,\: = X \\
\enspace\text{(T9D)} & X \ \cdot\ (X + Y) = X
\end{array}
& \text{Covering（吸收律）}
\\\\
\begin{array}{rl}
\text{(T10)} & \,\: X \ \cdot\ Y \,\: + \,\: X \ \cdot\ Y' \,\: = X \\
\text{(T10D)} & (X + Y) \ \cdot\ (X + Y') = X
\end{array}
& \text{Combining}
\\\\
\begin{array}{rl}
\text{(T11)} & \begin{aligned} & X \cdot Y + X' \cdot Z + Y \cdot Z \\[-0.2em] =\ & X \cdot Y + X' \cdot Z \end{aligned} \\
\text{(T11D)} & \begin{aligned} & (X + Y) \cdot (X' + Z) \cdot (Y + Z) \\[-0.2em] =\ & (X + Y) \cdot (X' + Z) \end{aligned}
\end{array}
& \text{Consensus}
\\\\
\begin{array}{rl}
\text{(T12)} & X + X + \cdots + X = X \\
\text{(T12D)} & X \ \cdot\ X \ \cdot\ \cdots\ \cdot\ X = X
\end{array}
& \text{Generalized idempotency}
\\\\
\begin{array}{rl}
\text{(T13)} &
\begin{aligned}
& (X \ \ \cdot\ X \ \ \cdot\ \cdots\ \cdot\ X)' \\[-0.2em]
= & \,\: X' + X' + \cdots + X'
\end{aligned}
\\
\text{(T13D)} &
\begin{aligned}
& (X + X + \cdots + X)' \\[-0.2em]
= & \,\: X' \cdot\ X' \cdot\ \cdots \ \cdot\ X'
\end{aligned}
\end{array}
& \begin{array}{c} \text{DeMorgan’s theorem} \\ \text{（摩根律）} \end{array}
\\\\
\begin{array}{rl}
\enspace\ \text{(T14)} &
\begin{aligned}
& [F(X_1, X_2, \ldots, X_n, +, \ \cdot\ )]' \\[-0.2em]
=&\ F(X_1', X_2', \ldots, X_n', \ \cdot\ , +)
\end{aligned}
\end{array}
& \begin{array}{c} \text{Generalized} \\ \text{DeMorgan’s theorem} \end{array}
\end{array} (T1) (T1D) X + 0 = X X ⋅ 1 = X (T2) (T2D) X + 1 = 1 X ⋅ 0 = 0 (T3) (T3D) X + X = X X ⋅ X = X (T4) ( X ′ ) ′ = X (T5) (T5D) X + X ′ = 1 X ⋅ X ′ = 0 (T6) (T6D) X + Y = Y + X X ⋅ Y = Y ⋅ X (T7) (T7D) ( X + Y ) + Z = X + ( Y + Z ) ( X ⋅ Y ) ⋅ Z = X ⋅ ( Y ⋅ Z ) (T8) (T8D) X ⋅ ( Y + Z ) = X ⋅ Y + X ⋅ Z X + Y ⋅ Z = ( X + Y ) ⋅ ( X + Z ) (T9) (T9D) X + X ⋅ Y = X X ⋅ ( X + Y ) = X (T10) (T10D) X ⋅ Y + X ⋅ Y ′ = X ( X + Y ) ⋅ ( X + Y ′ ) = X (T11) (T11D) = X ⋅ Y + X ′ ⋅ Z + Y ⋅ Z X ⋅ Y + X ′ ⋅ Z = ( X + Y ) ⋅ ( X ′ + Z ) ⋅ ( Y + Z ) ( X + Y ) ⋅ ( X ′ + Z ) (T12) (T12D) X + X + ⋯ + X = X X ⋅ X ⋅ ⋯ ⋅ X = X (T13) (T13D) = ( X ⋅ X ⋅ ⋯ ⋅ X ) ′ X ′ + X ′ + ⋯ + X ′ = ( X + X + ⋯ + X ) ′ X ′ ⋅ X ′ ⋅ ⋯ ⋅ X ′ (T14) = [ F ( X 1 , X 2 , … , X n , + , ⋅ ) ] ′ F ( X 1 ′ , X 2 ′ , … , X n ′ , ⋅ , + ) Identities （同一律） Null elements （零律） Idempotency （幂等律） Involution （双重否定律） Complements （补余律） Commutativity （交换律） Associativity （结合律） Distributivity （分配律） Covering （吸收律） Combining Consensus Generalized idempotency DeMorgan’s theorem （摩根律） Generalized DeMorgan’s theorem Shannon’s expansion theorems (T15) F ( X 1 , X 2 , … , X n ) = X 1 ⋅ F ( 1 , X 2 , … , X n ) + X 1 ′ ⋅ F ( 0 , X 2 , … , X n ) (T15D) F ( X 1 , X 2 , … , X n ) = [ X 1 + F ( 1 , X 2 , … , X n ) ] ⋅ [ X 1 ′ + F ( 0 , X 2 , … , X n ) ] \begin{array}{rl}
& \text{Shannon’s expansion theorems} \\[0.3em]
\text{(T15)} & F(X_1, X_2, \ldots, X_n) = \ X_1 \ \cdot\ F(1, X_2, \ldots, X_n) + X_1' \ \cdot\ F(0, X_2, \ldots, X_n) \\
\text{(T15D)} & F(X_1, X_2, \ldots, X_n) = [X_1 + F(1, X_2, \ldots, X_n)] \cdot [X_1' + F(0, X_2, \ldots, X_n)]
\end{array} (T15) (T15D) Shannon’s expansion theorems F ( X 1 , X 2 , … , X n ) = X 1 ⋅ F ( 1 , X 2 , … , X n ) + X 1 ′ ⋅ F ( 0 , X 2 , … , X n ) F ( X 1 , X 2 , … , X n ) = [ X 1 + F ( 1 , X 2 , … , X n )] ⋅ [ X 1 ′ + F ( 0 , X 2 , … , X n )] （ 草， 对齐好累， 我为什么要浪费这个时间。 ）
Duality 将一个等式中所有的 0 0 0 1 1 1 、 1 1 1 0 0 0 、 + + + ⋅ \cdot ⋅ 、 ⋅ \cdot ⋅ + + + ， 等式依然成立。
上面的定理中带 “ D” 的都是上一条的对偶。
Standard Representations of Logic Functions 这里需要翻出来我离散 (1) 写的 真值表生成器 （ 其实可以去加上 + + + ⋅ \cdot ⋅ ， 但如果要加 ′ ' ′ （
logic function 有若干精确的标准表示方法：
真值表
canonical sum: 主析取范式， 极小项 (minterm) 的和
使用 ∑ \sum ∑
canonical product: 主合取范式， 极大项 (maxterm) 的和
使用 ∏ \prod ∏
Verilog case 语句
这里用 ∏ \prod ∏ ： minterm 的 index 就是哪组变量取值下表达式值为 1， maxterm 的 index 就是哪组变量取值下表达式为 0， 所以两种范式的下标刚好是补集。 例如， 有 X , Y , Z X, Y, Z X , Y , Z ， X ′ ⋅ Y ⋅ Z ′ X' \cdot Y \cdot Z' X ′ ⋅ Y ⋅ Z ′ 2 2 2 ， X ′ + Y + Z ′ X' + Y + Z' X ′ + Y + Z ′ 5 5 5 ； ∑ X , Y , Z ( 1 , 2 , 6 ) = X ′ ⋅ Y ′ ⋅ Z + X ′ ⋅ Y ⋅ Z ′ + X ⋅ Y ⋅ Z ′ = ∏ X , Y , Z ( 0 , 3 , 4 , 5 , 7 ) \sum_{X,Y,Z}(1,2,6) = X' \cdot Y' \cdot Z + X' \cdot Y \cdot Z' + X \cdot Y \cdot Z' = \prod_{X,Y,Z}(0,3,4,5,7) ∑ X , Y , Z ( 1 , 2 , 6 ) = X ′ ⋅ Y ′ ⋅ Z + X ′ ⋅ Y ⋅ Z ′ + X ⋅ Y ⋅ Z ′ = ∏ X , Y , Z ( 0 , 3 , 4 , 5 , 7 ) 。
Verilog 的 case 语句大概是这个样子： （ 虽然还完全没学 Verilog， 但我感觉 Shiki 自带的 system-verilog 高亮看起来就比 verilog 正确许多， 以后可能也用 system-verilog 的高亮了）
case ( { X , Y , Z } ) 1 , 2 , 6 : F = 1 ; default: F = 0 ; endcase case ( { X , Y , Z } ) 1 , 2 , 6 : F = 1 ; default: F = 0 ; endcase Combinational-Circuit Analysis 这一节就是说给你一个电路图怎么搞出它的 logic function。 其实没啥好说的， 就（ 按拓扑序） 一个一个 gate 递推就行， 可以用真值表也可以用逻辑表达式。
有一个小 trick： DeMorgan’ s theorem 在电路图中表现为， 将 inversion bubble 换到另一侧（ 输入 / 输出） ， 并且改变 gate 的类型（ AND / OR） ， 这样的话， 如果两个 inversion bubble 在一条 wire 上就可以消掉。
Combinational-Circuit Synthesis 在 digital design 中， “ Synthesis” 有若干种含义（ 例如从 HDL 到 FPGA） ， 而在这一节只是指从 formal description 到 gate-level circuit。
Circuit Descriptions and Designs 自然语言描述 → 逻辑表达式 / 真值表（ canonical sum / product） → 电路
很多时候写出逻辑表达式会比列出真值表简单一些， 但在面对较为复杂的逻辑关系时， 列出真值表可以强制设计师考虑到每种情况， 从而避免漏掉 corner case。
一个输出是某个逻辑表达式的电路被称作 realize 了这个表达式， 是这个表达式的 realization 或者 implementation 。
Circuit Manipulations 在多数电路技术（ 包括 CMOS） 中， NAND / NOR 比 AND / OR 效率更高， 所以一般会修改电路来尽量使用 inverting gate 而非 noninverting gate：
在 wire 上移动 inversion bubble（ 从上一个输出移到下一个输入）
在 wire 的两侧同时加上 inversion bubble（ 或者 NOT gate）
消除同一根 wire 上的两个 inversion bubble
将 inversion bubble 换到另一侧（ 输入 / 输出） ， 并且改变 gate 的类型（ AND / OR）
Combinational-Circuit Minimization 一般情况下， 逻辑表达式的化简主要用的是定理 T10（ Combining） ， 就是在 sum of products 中找到仅有一项相反的两个 product 将它们合并， 最终得到的也是一个 sum of products， 实现为 2-level（ first-level 计算 product， second-level 计算 sum） 的电路。
product of sums 电路是对偶的， 就不重复了， 下文也是一样。
Karnaugh Maps 如 DDPP5 Figure 3-23 所示：
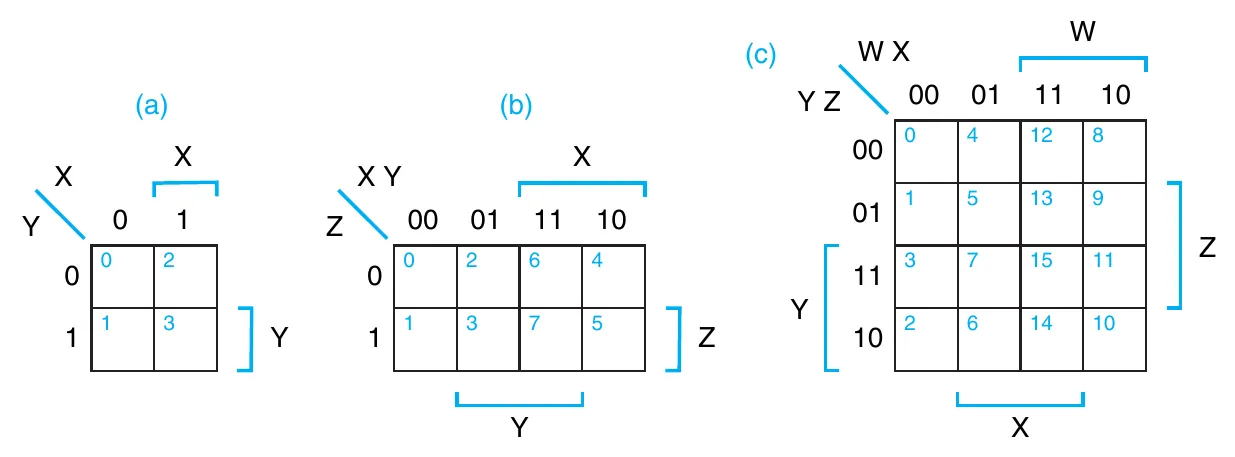
在 Karnaugh map 中， 每一个表示一个 minterm， 相邻（ 包括跨过边界到另一侧的相邻） 的格子仅有一位相反， 所以边长为 1 / 2 / 4 的矩形可以合并。
选出若干矩形， 恰好覆盖所有输出为 1 的格子， 就可以化简逻辑表达式。
如果一个矩形覆盖的全是 1， 并且是极大的（ 在其对应的 product 中减少任何一个输入都会使其覆盖到 0） ， 就称作一个 prime implicant 。 最简的逻辑表达式是若干 prime implicant 的 sum。
有的函数的 Karnaugh map 非常分散（ 例如 parity function） ， 没有连成一块的 1， 就需要多级而非 2-level 的电路来进行化简。
在 FPGA 中， 输入数量较少的电路都是通过 lookup table (LUT) 而非 gate-level circuit 来实现， 只需真值表就可以。 但复杂的电路需要由多个 LUT 组合起来， 此时逻辑表达式的化简依然有用。
Timing Hazards 真实的电路中会有 delay， 而上面研究的都是 combinational logic circuit 的 steady-state behavior ， 没有考虑到 transient behavior 。
因为 delay 的存在， 可能会发生这样的情况： 输入发生了改变， 稳态下的输出不变， 但在一瞬间内输出发生了变化（ 产生了一个 short pulse） 。 这样的 pulse 被称作 glitch 。
如果一个电路有产生 glitch 的可能性， 则称这个电路存在 hazard 。 实际物理电路的 delay 大小等因素难以控制， 所以这里只是考虑产生 glitch 的可能性， 而非实际是否有 glitch 产生（ 有点类似于并发编程中要保证所有可能的执行顺序下都不出错） 。
Static Hazards static-1 hazard ： 稳态输出是 1， 改变某一个输入后稳态输出还是 1， 但这一个输入改变时可能会短暂地输出 0。 static-0 hazard 是类似的。
书上给了个例子， 但这个其实很好理解， 就是电路的一个输入作为多个 gate 的输入， 而这些 gate 的输出变化得有快有慢。
Finding Static Hazards Using Maps 正常的 sum of products 电路中不会有 static-0 hazard， 可能有 static-1 hazard。
可以用 Karnaugh map 来找到 hazard： 如果两个相邻的 1 没有被同一个 gate 覆盖， 从其中一个变为另一个时就可能产生 glitch。 （ 因为极端情况下可能所有覆盖原来那一格的 gate 先全部变为 0， 覆盖后来那一格的 gate 才变为 1。 ）
消除 hazard 就是用冗余的 gate 来覆盖这样的相邻的 1， 类似于定理 T11（ Consensus） 。
Dynamic Hazards 如果变化一个输入时可能产生不止一次 glitch， 就称作 dynamic hazard 。
一个正常的 2-level sum of products / product of sums 电路中不会有 dynamic hazard。
Designing Hazard-Free Circuits 在多数电路中（ 尤其是 synchronous digital system 中） ， hazard 不会造成什么影响。 但在某些电路（ asynchronous sequential circuits） 中， 需要避免 hazard 的存在。
在一般的电路中消除 hazard 是复杂的， 而在 sum of products 中， 可以用 Karnaugh map 或者取遍所有 prime implicant（ 称作 complete sum ） 来消除 hazard。
