DDPP 第二章学习笔记

DDPP5 第二章 “Number Systems and Codes” 的学习笔记。

本章的主要内容为一些常用的编码以及纠错码的原理。

开头整数编码的内容很多是 CS:APP 第二章 讲过的，也有一些新内容，但基本上都是标星的可选内容，我看是看了但懒得写笔记了（

一套编码被称作一个 code，一个 code 中的单个合法编码（二进制串）被称作一个 code word。

Gray Code

Gray code 的性质：相邻两个数的 code word 只有一位不同，且 $2^n-1$ 的 code word 中只有一个 1（也就是说 $n$-bit Gray code 的首尾也只有一位不同）。

递归构造：

1. $1$-bit Gray code: 0 是 0，1 是 1
2. $(n+1)$-bit Gray code:
   • 前 $2^n$ 个数和 $n$-bit Gray code 相同（开头加上 0）
   • 后 $2^n$ 个数是把 $2^n$ 个 $n$-bit Gray code 逆序排列再在开头加上 1

直接计算单个数的 Gray code：

• 递归就能直接计算，相信大家都会做 NOIPD1T1 吧，记得开 unsigned long long（
• 也可以这么算：$n$ 的 Gray code 第 $i$ 位为 1 当且仅当 $n$ 的二进制中第 $i$ 位和第 $i+1$ 位不同

书中描述了一个使用场景：一个磁盘的每个扇区需要编码，从扇区上读取若干 bits 来识别当前处于哪个扇区，在两个相邻扇区的交界处可能有部分 bits 来自其中一个扇区，另外的 bits 来自另一个扇区，Gray code 可以使最终读取到的结果一定是这两个扇区之一。

Codes for Actions, Conditions, and States

说白了就是如何编码一个 enum。不同的编码方式有各自的特点，可以从编码长度、电路开销、设计难度、可纠错性等角度考虑，选择最合适的编码方式，或者组合使用多种编码方式。

• 顺着编码为二进制可以使编码长度最短（$\lceil \log_2 n \rceil$）。
• 1-out-of-n-code：合法的 code word 只有一位是 1，每个 enum 对应某一位为 1。例如，控制哪个灯开时，这种编码方式无需再有电路来选择要开的灯，直接将编码的每一位连到一盏灯就可以了。
• m-out-of-n-code：合法的 code word 恰有 $m$ 位是 1。要检测一个 code word，只需使用一个 $m$-input AND gate，电路较为简单。而 code word 总数有 $\binom nm$，也很多。

n-Cubes and Distance

以 $2^n$ 个 $n$-bit 二进制串作为顶点，在只有一个 bit 不同的串之间连边，得到的图被称作 $n$-cube，可以画成一个（超）立方体：（DDPP5 Figure 2-8）

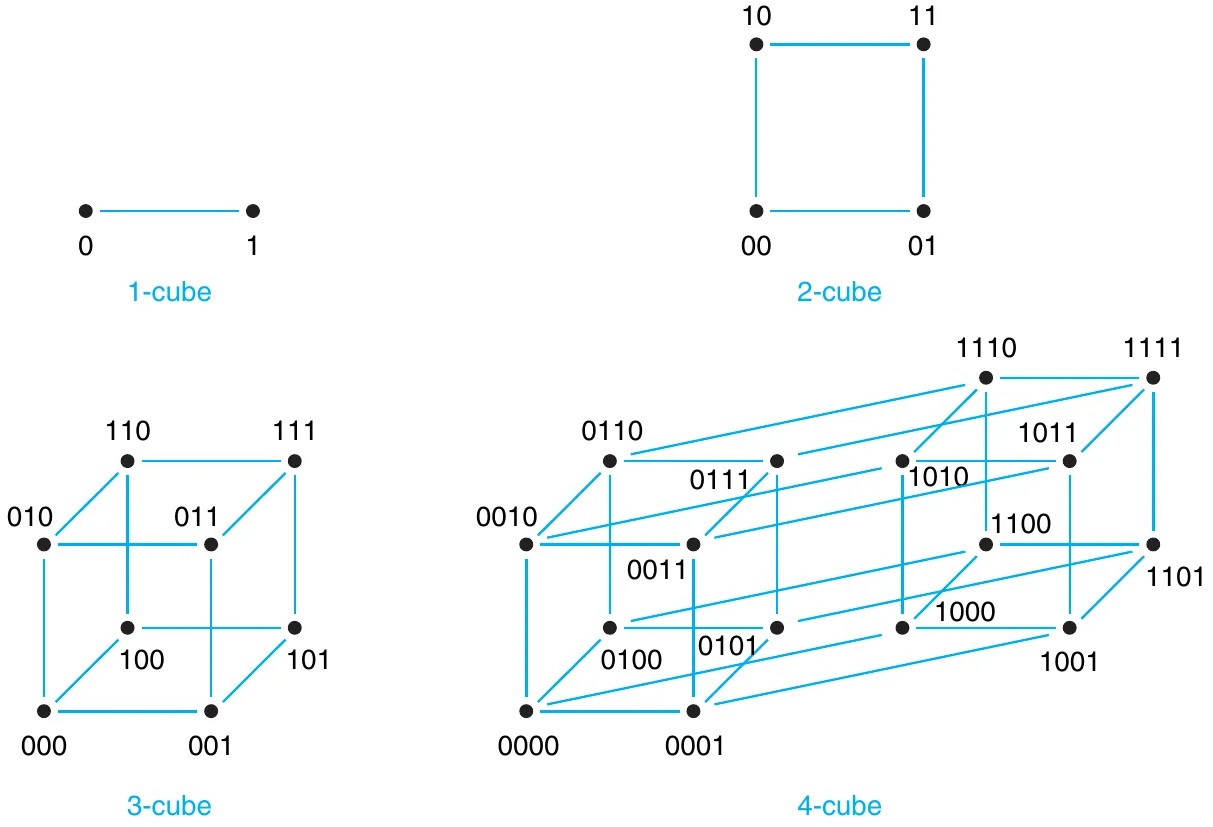
图上两个二进制串之间的距离被称作 Hamming distance，表示两个串中不相同的位数。

Codes for Detecting and Correcting Errors

实际存储、传输编码时，可能会发生错误。错误的具体行为可以由 error model 刻画。最简单的 error model 是 independent error model，即每个错误只独立地改变编码中的一位，多位同时发生错误的概率比一位发生错误的概率小得多。

Error-Detecting Codes

对于一个 code，不是 code word 的二进制串称作 noncode word。

error-detecting code 具有这样的性质：任何一个 code word 在任意修改一位后都会得到一个 noncode word。

使用 error-detecting code 时，可以认为只要是 code word 都没有发生错误，noncode word 则一定发生了错误。

一个 $n$-bit error-detecting code 是 $n$-cube 的一个点独立集，也就是说任意两个 code word 的 Hamming distance 都至少为 2。

奇偶性可以用来设计 error-detecting code：任给一个 $n$-bit code，将第 $n+1$ 位设为前 $n$ 位中 1 的个数的奇偶性（称作 parity bit），则可以得到一个 $(n+1)$-bit error-detecting code。这样的编码称作 1-bit parity code，若 code word 都有偶数个 1 则称作 even-parity code，有奇数个 1 则称作 odd-parity code。

Error-Correcting and Multiple-Error-Detecting Codes

如果一个 code 中两个 code word 的最小 Hamming distance 有 $2c+d+1$，则可以对最多 $c$ 位的错误进行纠正，并且检测到最多 $c+d$ 位的错误（一个 $c+d+1 \sim 2c+d$ 位的错误会被认为是来自另一个方向的错误而被错误地纠正，从而不能被检测到；可以选择少纠错几位来检测到更多位的错误）。

纠错就是找到和一个 noncode word 的 Hamming distance 最小的唯一一个 code word，进行纠错的硬件被称作 error-correcting decoder。

Hamming Codes

Hamming code 是一种通用的最小距离为 3 的编码。一个有 $n$ 个 check bit 的 Hamming code 最多可以存储 $2^n-n-1$ 个 information bit，从而总共有 $2^n-1$ 个 bit。

一个 $(2^n-1)$-bit Hamming code 的 bit 依次编号为 $1 \sim 2^n-1$，编号为 $1, 2, 4, \ldots, 2^{n-1}$ 的 bit 是 check bit。每个 check bit 代表一个 group，编号为 $2^i$ 的 check bit 所代表的 group 包含的是编号的二进制中包含 $2^i$ 的所有 bit。check bit 的取值使得每个 group 都含偶数个 1。

实际使用的 Hamming code 往往会将 check bit 移到末尾，例如一个 $15$-bit Hamming code 中 bit 的编号依次为 15, 14, 13, 12, 11, 10, 9, 7, 6, 5, 3, 8, 4, 2, 1。

因为每个 bit 都至少属于一个 group，改变一个 bit 会得到 noncode word。改变编号为 $i$ 和 $j$ 的两个 bit 时，会改变 $i$ 异或 $j$ 对应的 group，所以改变两个 bit 会得到 noncode word。所以 Hamming code 中两个 code word 的 Hamming distance 至少为 3。

纠错时，只要将错误的 check bit 的编号或起来就可以得到错误的 bit 的编号。

可以通过增加一个 parity bit 来得到一个最小距离为 4 的 $2^n$-bit extended Hamming code。

CRC Codes

cyclic-redundancy-check (CRC) codes 是一种得到广泛应用的 error-correcting code，例如被用在文件系统和网络通信中，它可以检测到成团出现的多位错误，在一些场景中这种错误比随机出现的错误概率更高。

Two-Dimensional Codes

如 DDPP5 Figure 2-14 (a) 所示：

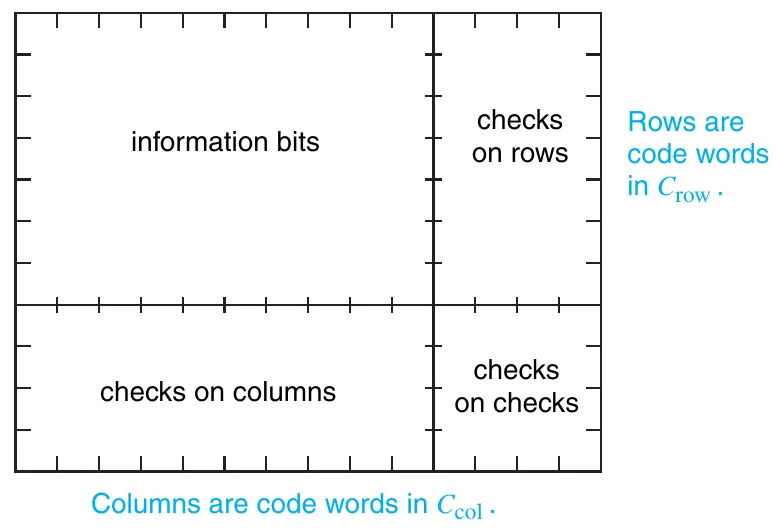
选择 $C_{\mathrm{row}}$ 和 $C_{\mathrm{col}}$ 两种编码方式，设置 checks on rows 使得 information bits 所在的每一行都是一个 $C_{\mathrm{row}}$ 的 code word，设置 checks on columns 使得 information bits 所在的每一列都是一个 $C_{\mathrm{col}}$ 的 code word，而 checks on checks 则可以选择，要么每一行都是一个 $C_{\mathrm{row}}$ 的 code word，要么每一列都是一个 $C_{\mathrm{col}}$ 的 code word。

这样得到的 two-dimensional code 的最小距离是 $C_{\mathrm{row}}$ 和 $C_{\mathrm{col}}$ 的乘积，所以 two-dimensional code 也被叫做 product code。

RAID 就可以看作使用了 two-dimensional code：每块数据盘内的每个 block 都有 CRC code，还有一块硬盘用来存所有数据盘的 parity bits。

Checksum Codes

parity bit 可以看作是 bits 在模 2 意义下的和，可以推广为 checksum。

例如，模 256 意义下，可以计算 bytes 的和，来检测 bytes 的错误。

除了改变模数，还可以改变计算方式，例如使用 ones’ complement 加法来计算模 255 或 65535 意义下的 checksum。

m-out-of-n Codes

m-out-of-n code 的最小距离为 2，并且能够检测到 unidirectional multiple errors，即所有错误都是 0 变 1 或 1 变 0 的改变多位的错误。

Codes for Transmitting and Storing Serial Data

• parallel data transmission: 一个 data word 的所有 bit 同时传输
• serial data transmission: 一个 bit 一个 bit 传输

在某些场景下，serial data transmission 可以减少线路开销，或者减少一些设计上的困难。

最基本的 serial data transmission 需要三个信号：

• CLOCK: 将时间划分为一个个 bit cell，标识出每个 bit 所处的时间范围
• SERDATA: 实际传输的数据，具体内容依 line code 而定
• SYNC: 用来标识 bit 的 significance，例如传输 bytes 时用来标记每个 byte 的开头

实际上，也可以选择合适的 line code 从而只需传输一个信号，从数据信号中读取出 CLOCK 和 SYNC 的信息。